Musées et archives
Le mécanisme est conservé au Musée polytechnique (Moscou, Russie); dépôt, PM № 19461.
Le mécanisme est conservé au Musée des arts et métiers du Conservatoire national des arts et métiers (Paris); CNAM № 11472-0007.
Le mécanisme est conservé au Musée d’histoire de la physique et des mathématiques de l’Université d'État de Saint-Pétersbourg (Peterhof, Russie).
Articles originaux de Tchebychev
Sur le système articulé le plus simple donnant des mouvements symétriques par rapport à un axe / D’après: Œuvres complètes de P. L. Tchebychev. Tome IV. Théorie des mécanismes. — Moscou-Léningrad: AS URSS. 1948. P. 167-211. (En russe)
Recherches
I. I. Artobolevski, N. I. Levitski.. Mécanismes de Tchebychev / Dans: Héritage scientifique de P. L. Tchebychev. Fasc. 2. Théorie des mécanismes. — Moscou-Léningrad: AS URSS. 1945. P. 30–32. (En russe)
I. I. Artobolevski, N. I. Levitski.. Modèles des mécanismes de P. L. Tchebychev / Dans: Œuvres complètes de P. L. Tchebychev. Tome IV. Théorie des mécanismes. — Moscou-Léningrad: AS URSS. 1948. P. 215–217. (En russe)
Autres sources
Engins inventés par l’académicien Tchebychev // Vsemirnaya Illustratsia (Illustration d’universel). 1893. № 1275. P. 17. (En russe)
Description
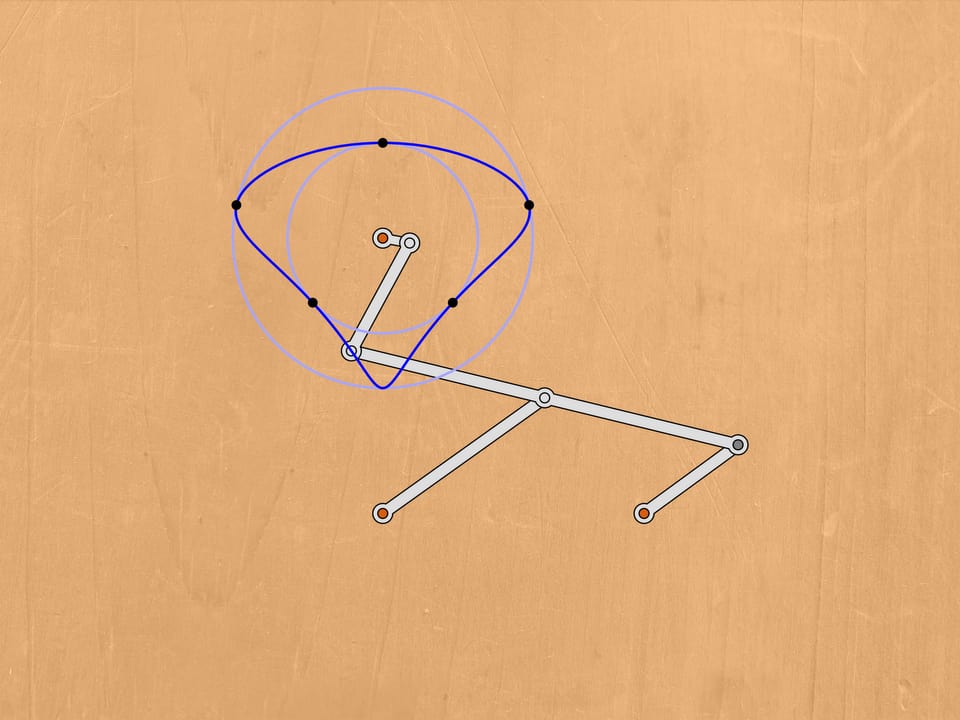
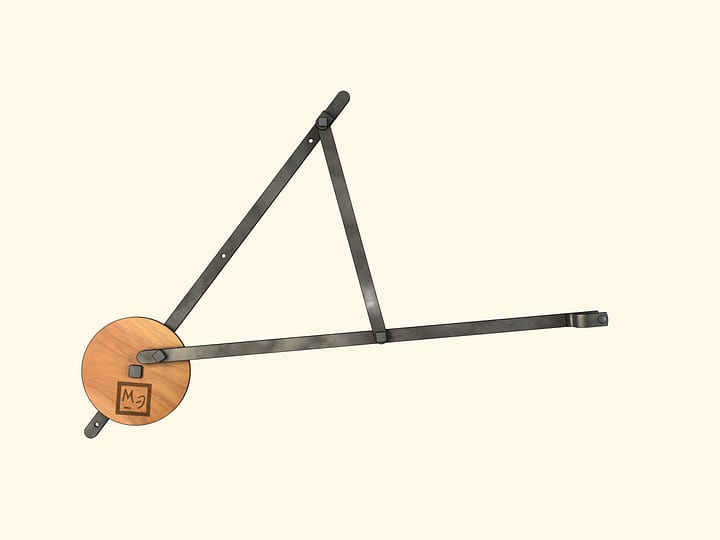
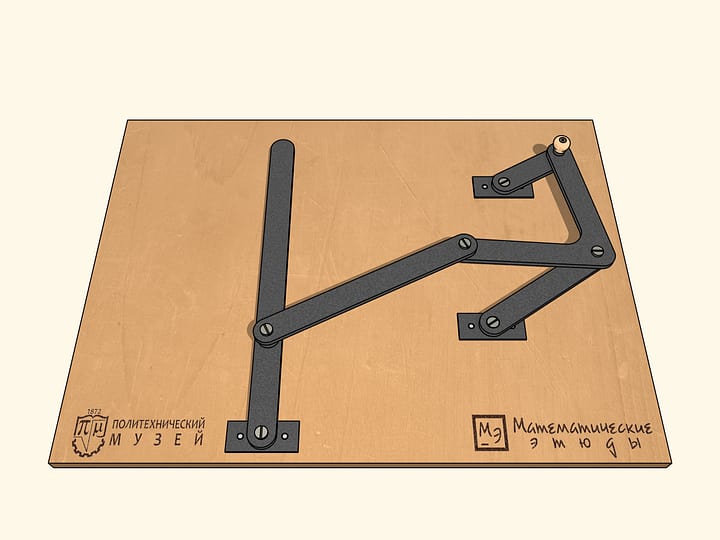
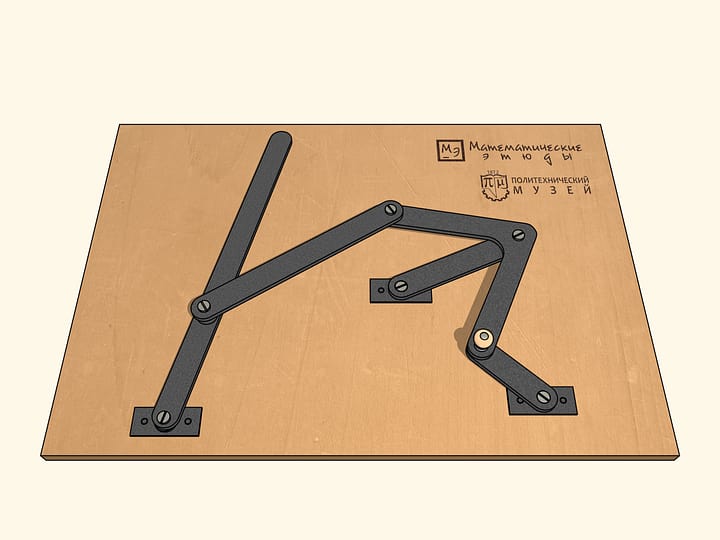
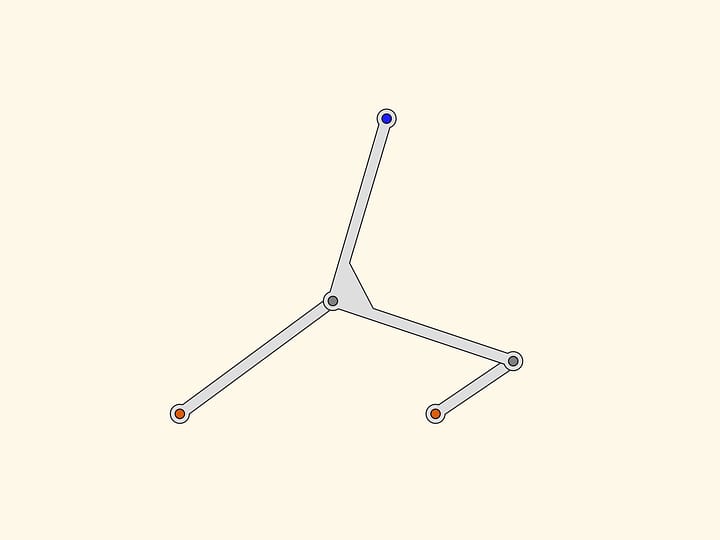
Quelles images peuvent être réalisées par l’application représentée dans la figure, avec une charnière fixe (rouge)?
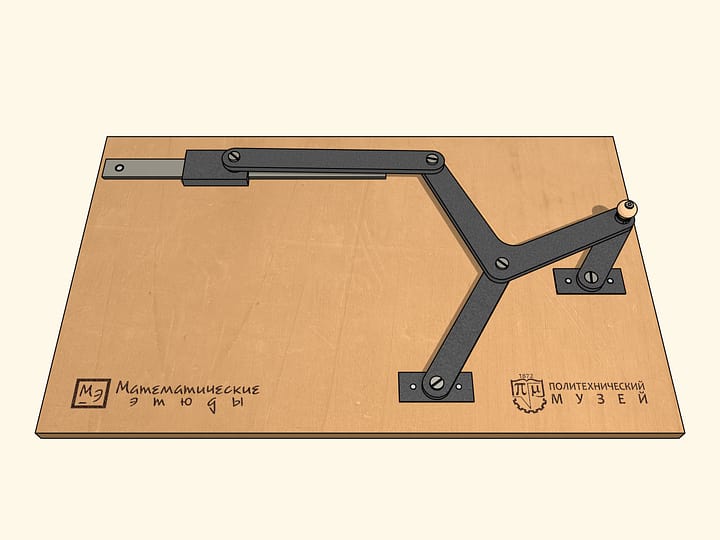
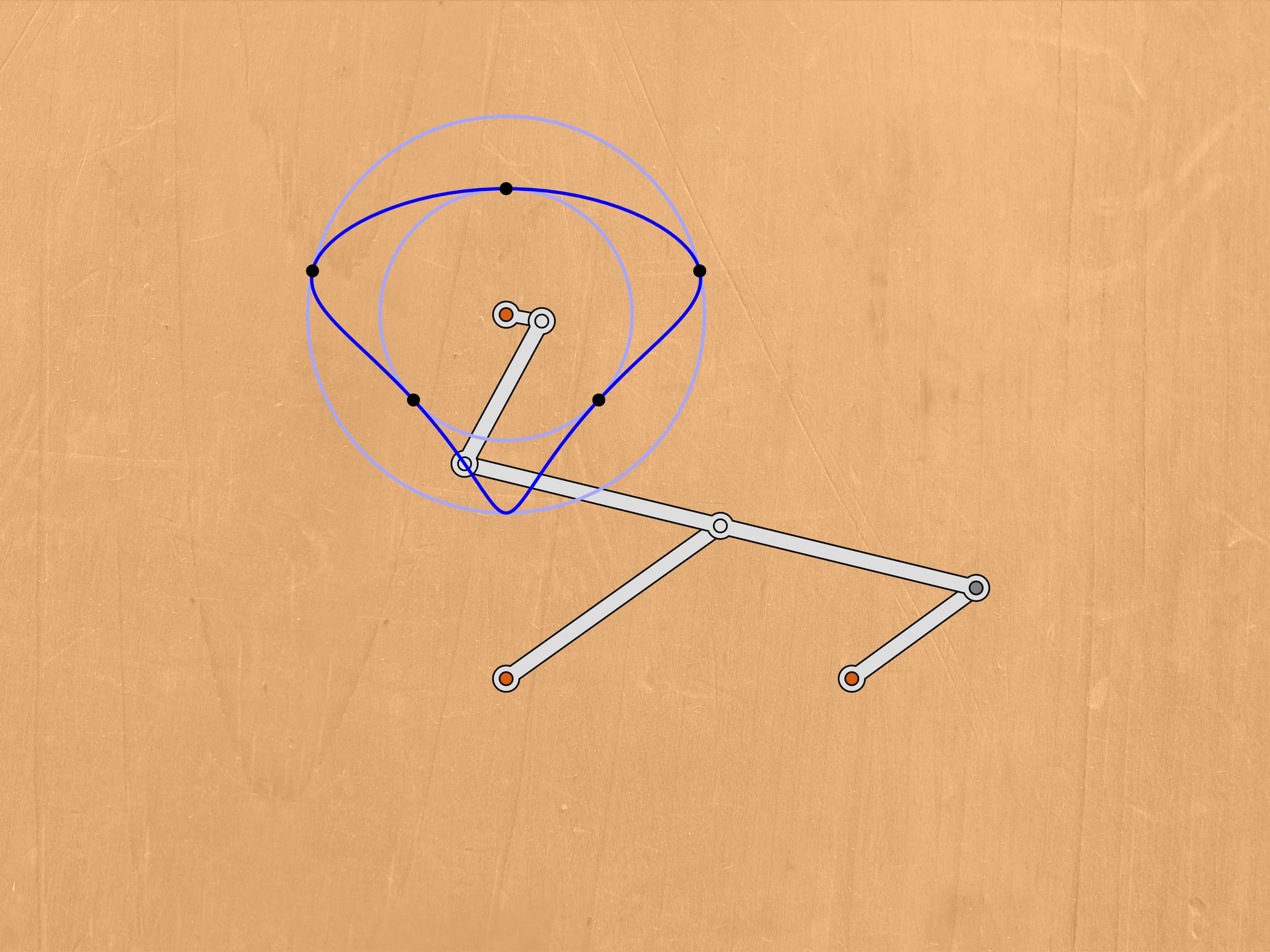
Laissons que la charnière marquée en gris glisse le long d’une courbe, symétrique par rapport à une droite passant par la charnière fixe. On peut montrer que dans ce cas aussi la trajectoire de la charnière en bleu sera symétrique par rapport à une droite passant par la charnière fixe. Le mathématicien russe Pafnutiy Lvovitch Tchebyshev se posa le problème de trouver quelle est cette trajectoire.
Un cas particulier et important se produit lorsque la trajectoire en gris est un cercle. Dans la pratique, on obtient cela en ajoutant une autre charnière fixe (rouge) et une barre de guidage d’une certaine longueur.
Pour la trajectoire en bleu, il ya deux cas importants: quand c’est un segment de droite, et quand c’est un cercle, ou un arc de cercle.Tchebyshev écrit: «Ici, nous allons examiner les cas les plus simples, et aussi plus fréquent dans la pratique, précisément lorsque on veut se déplacer le long d’une courbe, dont une partie, plus ou moins importante, diffère peu d’un arc ou d’une ligne droite».
Juste pour trouver les meilleurs paramètres de ce mécanisme qui résout les problèmes énumérés, Tchebyshev appliqua pour la première fois la théorie de l’approximation des fonctions, qu’ il avait lui–même développée en étudiant le parallélogramme de Watt.
En choisissant de façon appropriée la distance entre les charnières fixes, la longueur de la barre de guidage, et l’angle entre les deux barres, Tchebyshev obtint une trajectoire fermée, qui s’éloigne peu d’un segment de droite. L’écart par rapport à une trajectoire rectiligne peut être diminué en changeant les paramètres du mécanisme. Cependant, ce changement des paramètres va aussi conduire à une diminution de la longueur de la trajectoire tracée par la charnière en bleu. Puisque cette diminution est moins rapide que la diminution de l’écart du segment rectiligne, dans les problèmes pratiques on peut toujours trouver des paramètres satisfaisants. Ceci est seulement un des mécanismes à charnières pour tracer approximativement des segments de droite, qui ont été proposés par Tchebyshev.
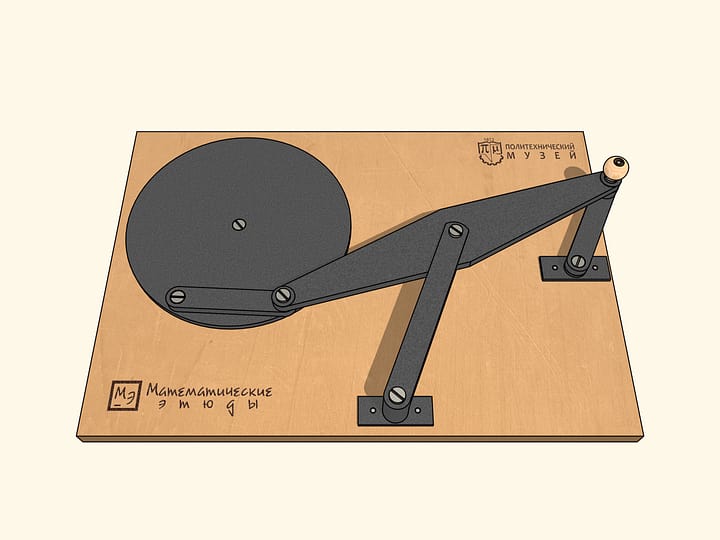
Considérons maintenant le au cas où la courbe bleue est un cercle.
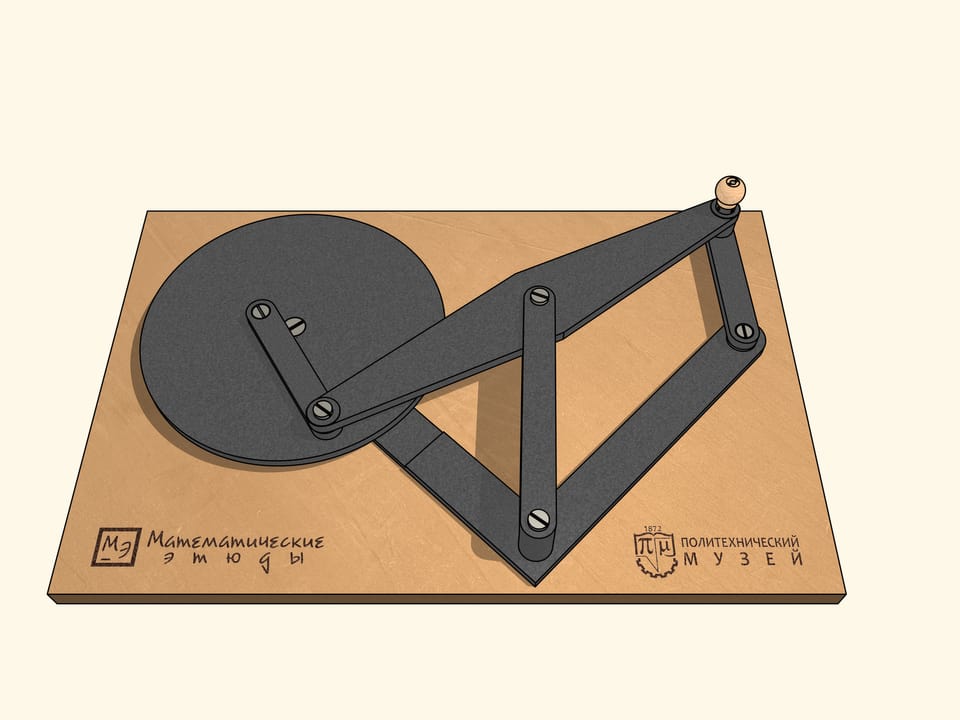
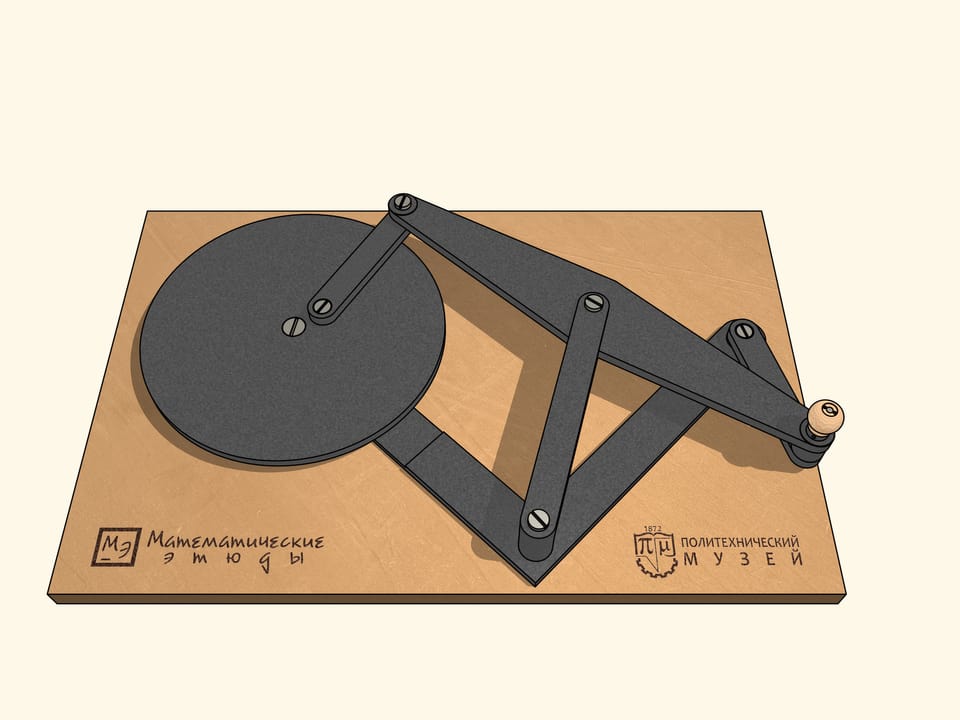
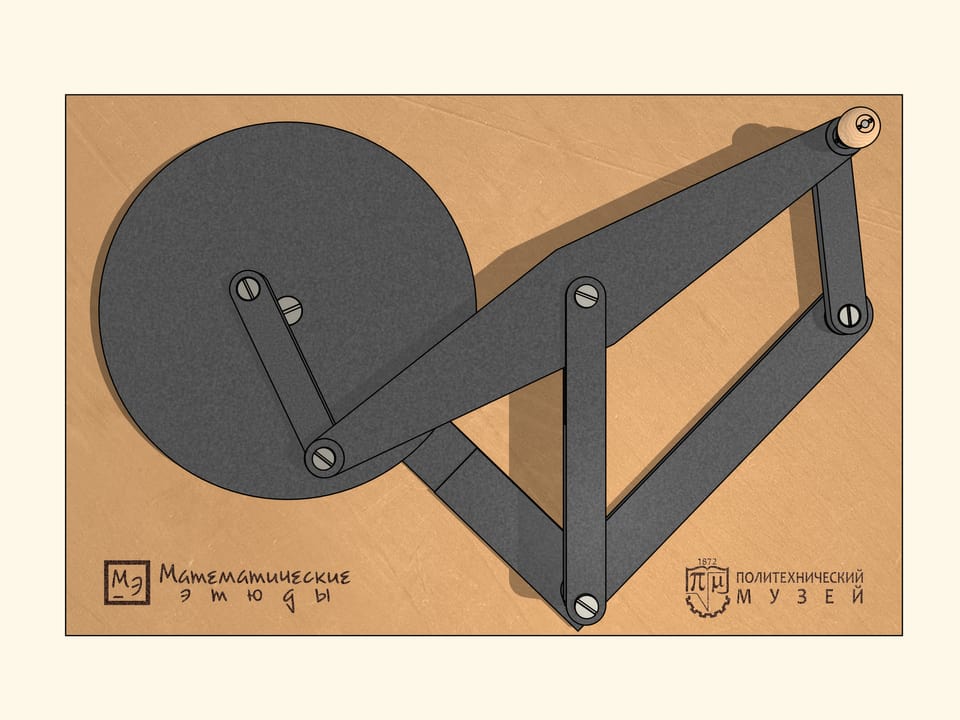
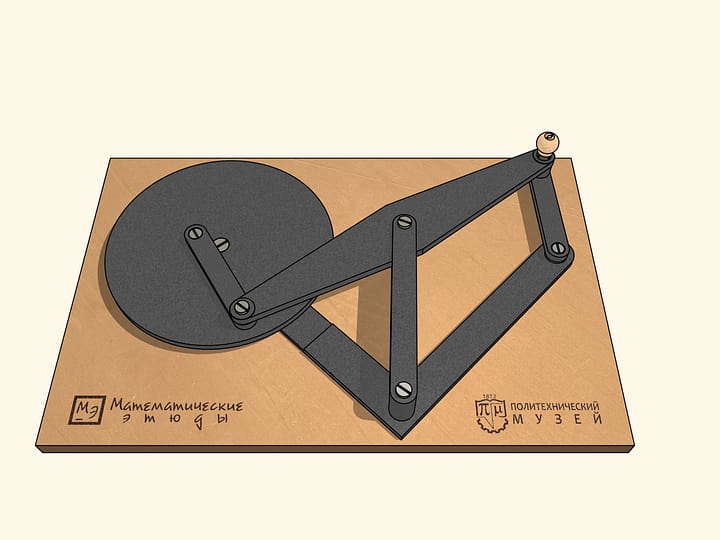
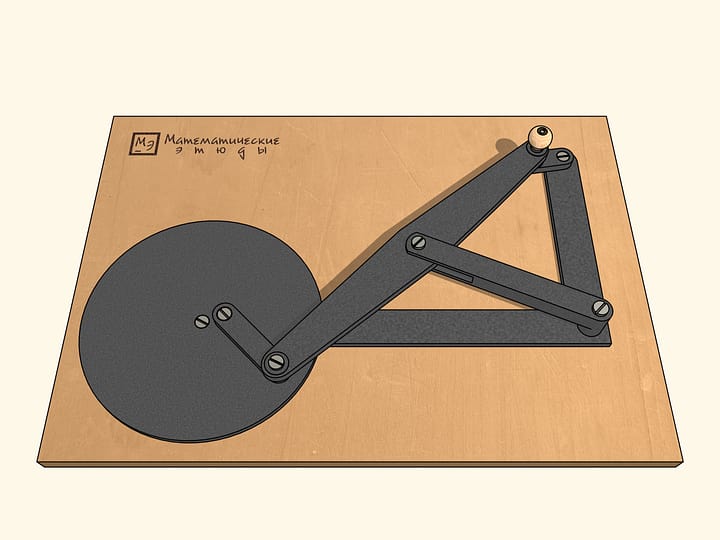
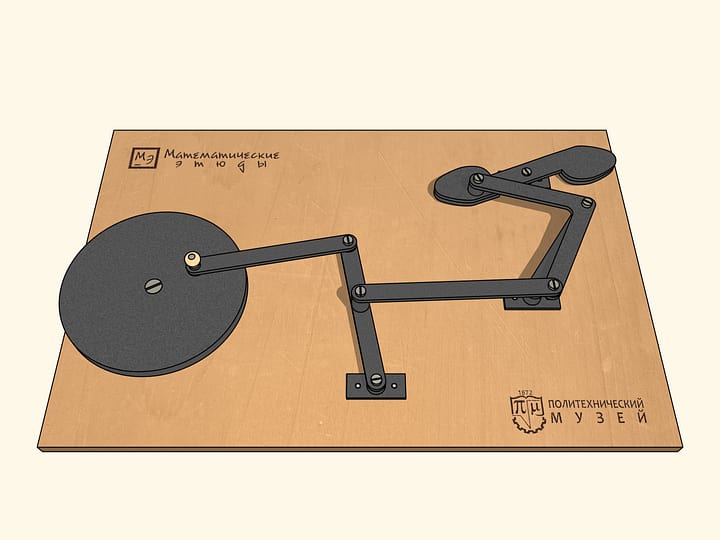
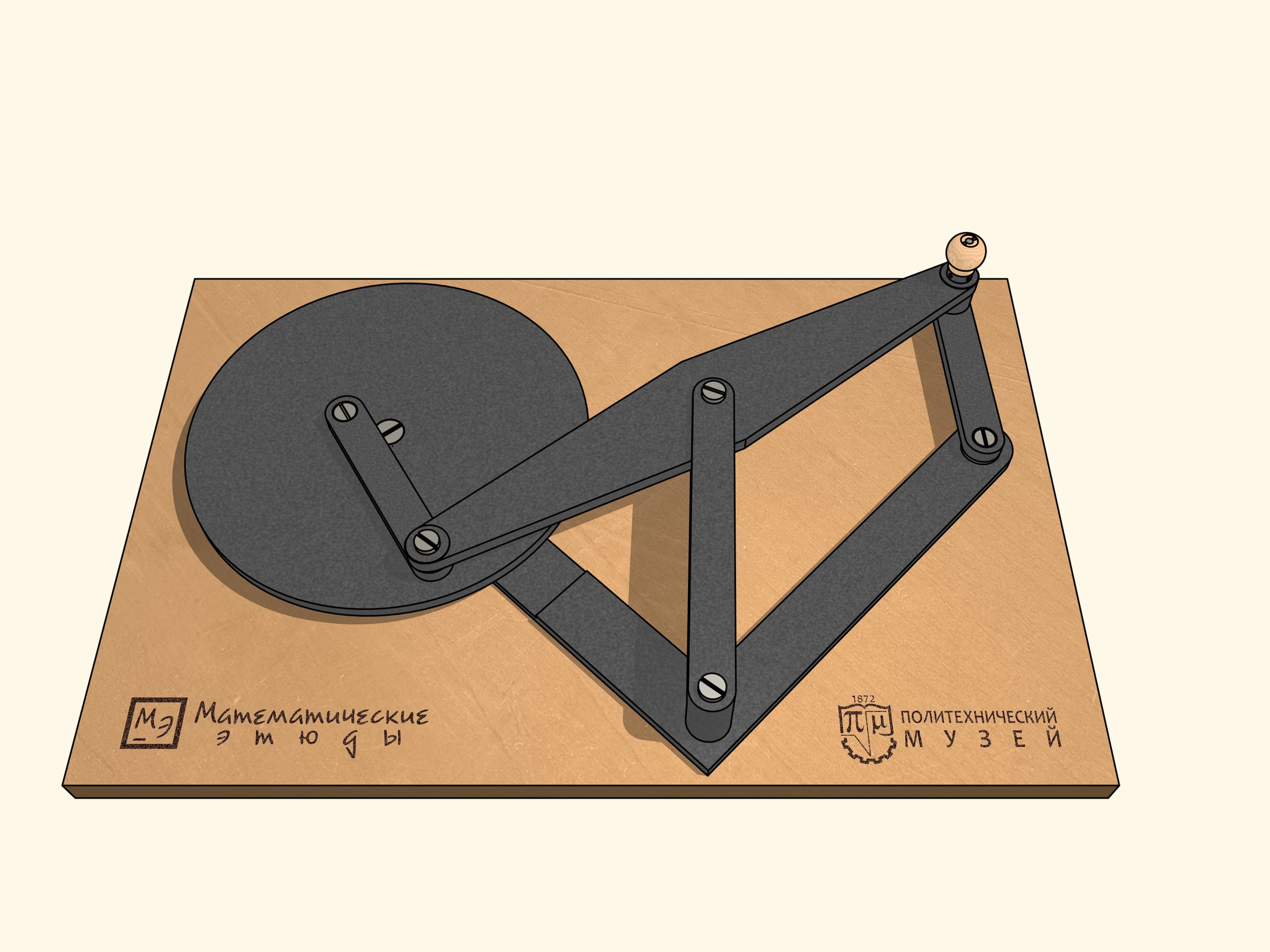
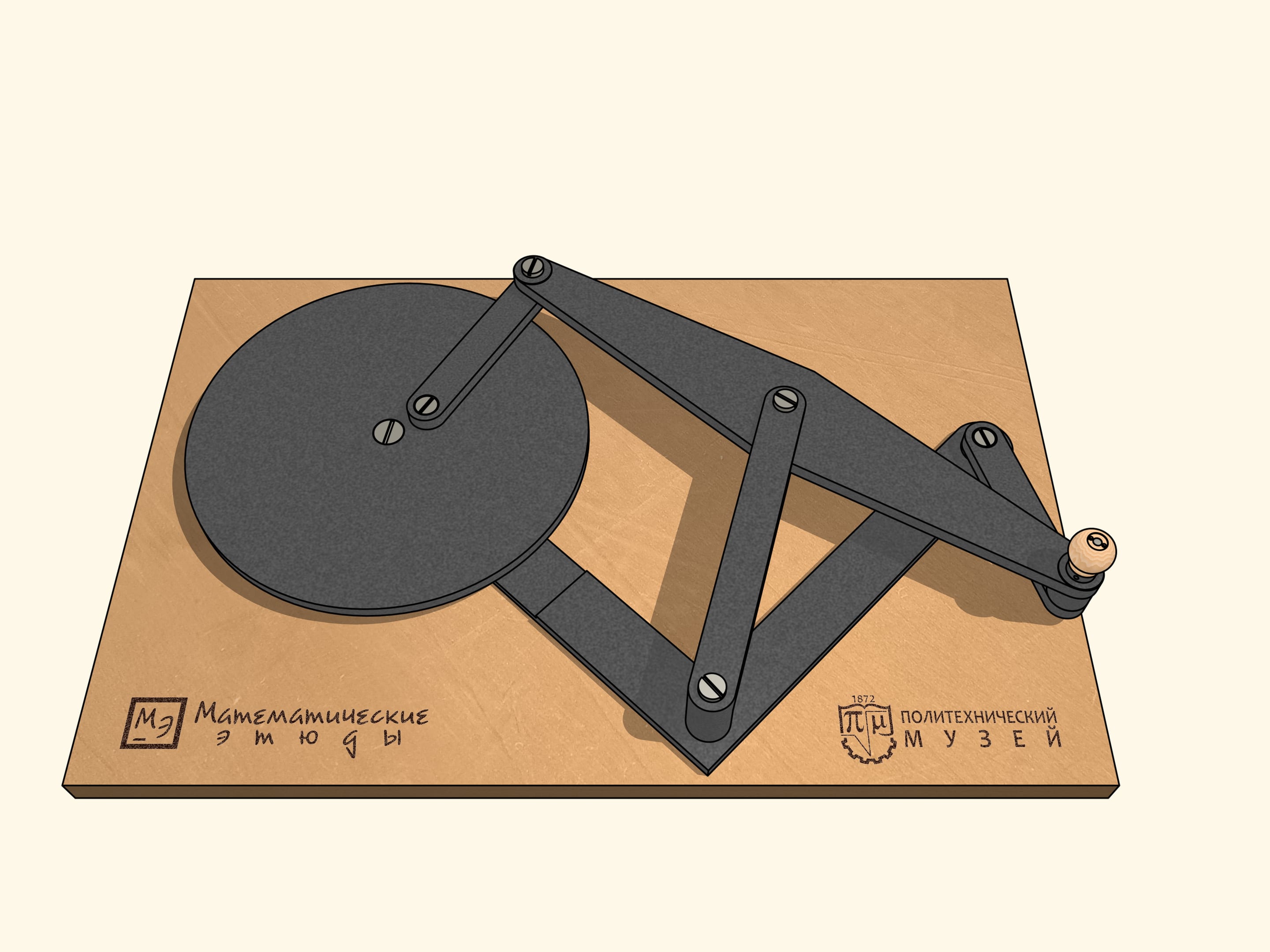
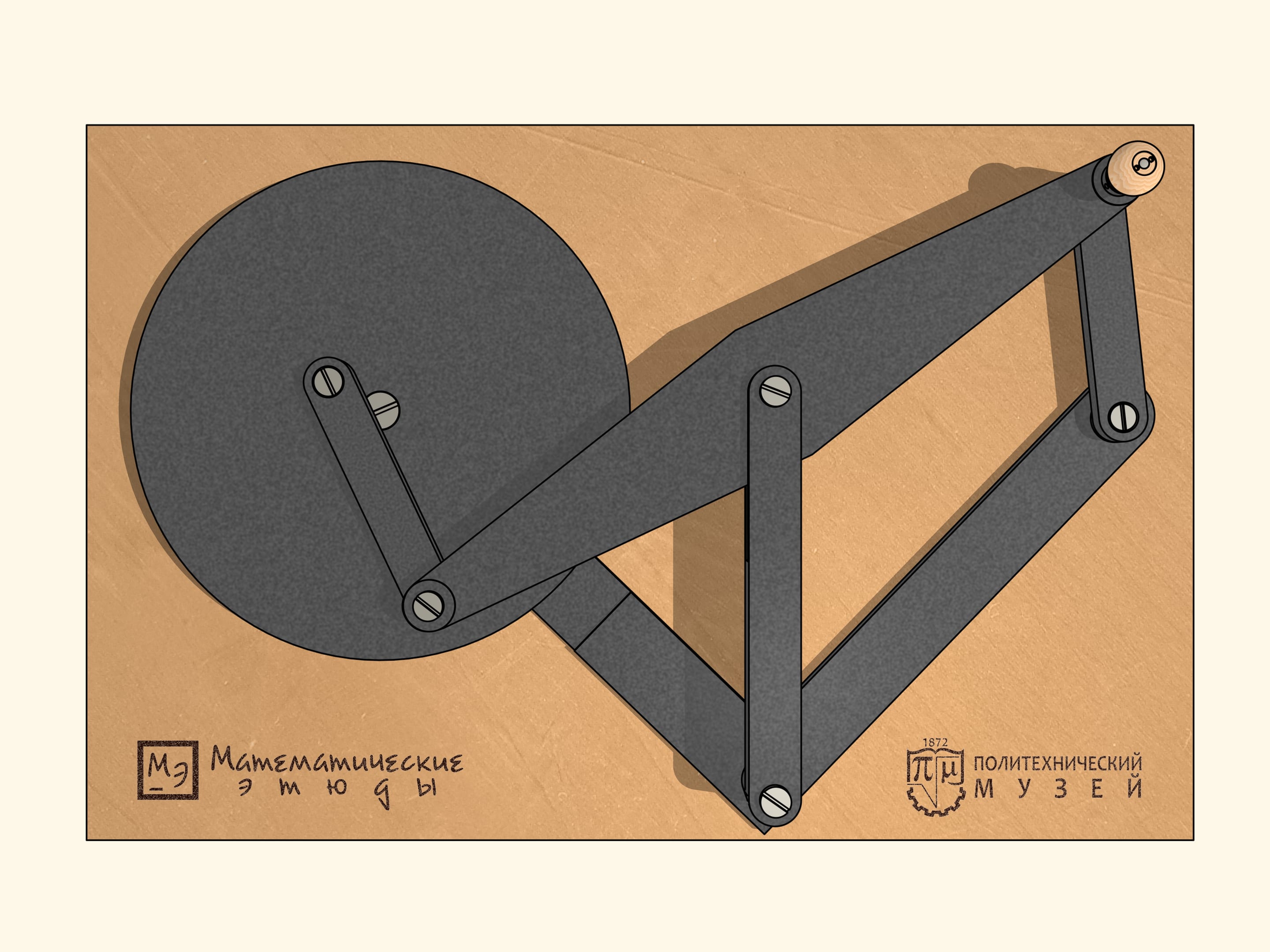
Lorsque les barres sont sur la même ligne, notre mécanisme est similaire à la lettre grecque «lambda». Tchebyshev l’avait utilisé avec des paramètres appropriés pour construire la première «machine plantigrade». Dans ce cas, la courbe bleue ressemble au chapeau d’un champignon. En choisissant différemment les paramètres du mécanisme, on peut obtenir une trajectoire qui est tangente à deux cercles concentriques alternativement, en restant tout le temps entre un et l’autre. En changeant les paramètres du mécanisme, on peut réduire la distance entre ces cercles concentriques, entre lesquels la trajectoire bleu se trouve.
Pour terminer la construction du mécanisme à lambda, nous ajoutons une charnière fixe et deux barres, dont la somme des longueurs est égale au rayon du cercle plus grand, et la différence au rayon du cercle plus petit.
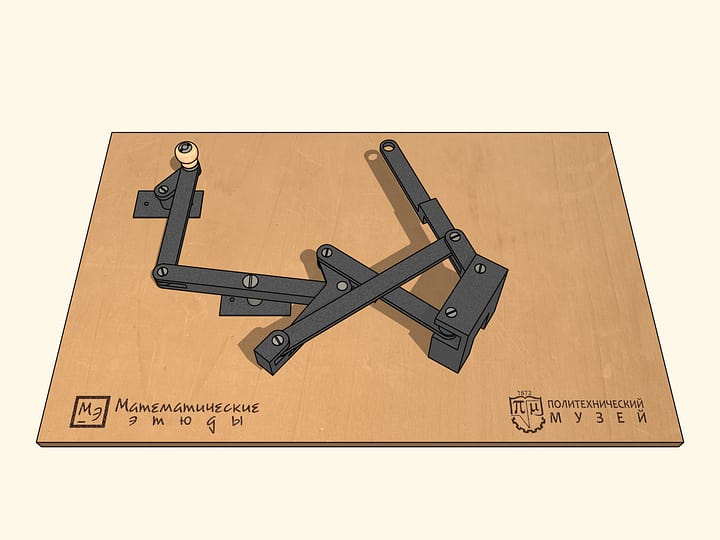
L’appareil qui en résulte a des points de bifurcation, ou, en d’autres termes, des points singuliers. Lorsqu’on se trouve dans un de ces points, par le mouvement même du mécanisme dans le sens des aiguille d’une montre, les bars ajoutées commencent à tourner à la fois dans le sens des aiguilles d’une montre, à la fois dans le sens inverse. De ces points de bifurcation notre mécanisme en possède exactement six, lorsque les barres ajoutées se trouvent sur la même ligne droite.
Il existe un domaine important des mathématiques — la théorie des singularités — à savoir, l’étude d’un objet à travers l’analyse de ses points singuliers. Un cas particulier très simple c’est l’étude du comportement des fonctions à travers l’analyse de leurs points de maximum et de minimum.
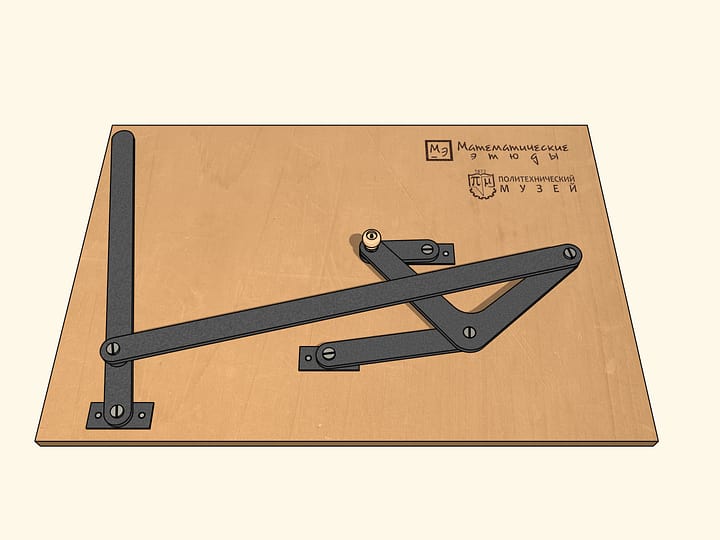
Pour que notre mécanisme passe à travers les six points singuliers dans un sens choisi au début, la barre petite est relié à un volant, qui, tournant dans ce sens, guide le mécanisme à tourner dans le même sens à tous les points singuliers.
Si le volant, ainsi que la barre, est déplacé du point de bifurcation dans les sens des aiguilles d’une montre, à chaque tour de la barre de guidage le volant fera deux tours.
Si au contraire le volant est déplacé du point de bifurcation dans les sens inverse des aiguilles d’une montre, à chaque tour de la barre de guidage le volant fera quatre tours!
C’est là que le paradoxe de ce mécanisme, inventé et fabriqué par Pafnuty Chebyshev, réside. Il semblerait qu’un mécanisme doit fonctionner d’une façon unique, cependant , comme nous l’avons vu, n’est pas toujours le cas. Et la raison c’est la présence de points singuliers.